Consider these questions:
- 3361 × 100 = 336100
- 3.361 × 100 = 336.1
- 33.61 × 100 = 3361
- 0.3361 × 100 = 33.61
- 336.1 × 100 = 33610
To a maths teacher, or a pupil who achieved old-money KS2 level 5 in maths, these are utterly trivial questions that require barely any conscious thought.
Yet to any pupil who finds maths difficult, these questions can be bewildering.
On the surface they are all the same process – ×100 – yet the process performed on each number looks radically different. Take question 1: 3361 × 100. Simple, right? Put an extra two zeros at the end of the number, and it’s right. But apply that process to questions 2, 3, and 4, and you’ll get it totally wrong. Question 2: 3.361 × 100. Similarly simple: all you have to do is move the decimal place two places to the right . But in question 3, the decimal point has disappeared altogether in the answer – where’s it gone?! Then over to question 4 and 5, and two weird things happen: whilst the decimal points have moved as expected, a zero has disappeared from the left of the number, whereas in question 5, a zero has appeared on the right of the number.
To illustrate: have a look at these mistakes, and see if you can spot the inferences made:
- If 3361 × 100 = 336100, then: 3.361 × 100 = 3.36100
- If 33.61 × 100 = 3361, then 0.3361 × 100 = 03361
- If 3.361 × 100 = 336.1, then 336.1 × 100 = 3361 .
Of course pupils find it bewildering.
I’ve started to think that this topic is a great example of mathematical grammar, and as such, requires a specific form of teaching for pupils to learn it well. What do I mean by this? And how can we help pupils get it?
When I first saw my pupils making errors when multiplying and dividing by powers of 10, my first instinct was to gently cajole them: ‘look this is easy, just move the decimal point this many times’. Yet implicit in my answer would be any number of things: for example, I’d remove unnecessary placeholder zeros, or fill in placeholder zeros, or make decimal points disappear. What was I doing? Over-simplifying and over-generalising, at the same time. In fact, in my head, I was doing a massive number of things – I wasn’t ‘just’ moving a decimal point. Implicit in my personal sense of ease was an expert understanding of the number system, of place value, and of number-system-notation conventions. None of that is easy or straightforward! Yet it seemed easy to me, because of ‘the curse of knowledge’. What we know is utterly transparent to our minds, such that we don’t even realise that we know it or that our reasoning is built upon it.
Something similar seems to happen in learning grammar. Daisy Christodolou’s blog on grammar provides very useful parallels.
How does one explain to a pupil like this where to use full stops, or apostrophes? In her own words:
We have to start with the basics… We need to get them to appreciate, first of all, what a sentence is. And to understand what a sentence is, you have to know what a verb is and what a subject is. How do we get pupils to know what a verb and a subject are? These are not simple concepts…
If you look at the sheer amount of stuff that is necessary just for a basic understanding of a simple sentence, you will see firstly that you need to spend quite a lot of class time on this, and secondly that pupils will need to memorise a lot of the rules and processes. They will need to memorise the rules and processes in order to free up space in working memory so that when they come to write their own simple sentences, the process is as automatic as possible. They also need to memorise the rules and processes because grammar goes on to get a lot more complicated than this, and they need the basic rules well established in long-term memory so that the more advanced rules can build on these without taking up too much space in working memory.
Daisy’s view, in short: the basic understanding required for foundational topics, like sentences, is huge; and so it requires lots of class time devoted to memorising certain rules, procedures and concepts.
Katie Ashford makes the same point about apostrophes in a brilliant blog here:
When teaching something as seemingly straightforward as the humble apostrophe, we can underestimate the amount of knowledge required to really understand it. In order to use an apostrophe correctly, pupils need to understand five complex, overlapping rules:
- Singular and plural nouns not ending in ‘s’: show possession by adding apostrophes.
- Singular and plural nouns ending in ‘s’: show possession by adding an apostrophe (and sometimes an extra ‘s’ at the end).
- Plural nouns that don’t possess anything do not require an apostrophe.
- Pronouns of possession do not require an apostrophe.
- Contracted verbs/nouns: show omission by adding an apostrophe in place of the missing letters.
To teachers, it seems trivial knowing where to put full stops or apostrophes… yet when you start to try and explain it, it suddenly starts to seem rather reliant on deep, embedded understandings.
The same issue is true for teaching × 100. Let’s make it concrete: here are some rules, procedures, and concepts pupils need to know to answer expertly questions 1-5 on × 100.
- The convention of leaving blank the place value columns which are of greater value than the value of a number (i.e. not writing zeros on the left of numbers greater than zero). E.g. to write 36, instead of 0036.
- The convention of filling zeros into place value columns in order to express certain numbers greater than 10 and less than 0.1 (i.e. to write zeros on the right of numbers and on the left of numbers). E.g. to know the necessity of the zeros in 3600 and 0.00036.
- The equality of value between 5 and 5.0 and 5.00 etc, and the convention of writing integers without decimal points and placeholder zeros, and at the same time the usefulness of re-expressing integers with these decimal points and placeholder zeros.
- The convention of having invisible decimal points on the right of integers, e.g. not writing ‘5.’ but ‘5’ instead.
- (For that matter, the definition of integers!)
- Multiplication by powers of 10 means moving decimal points sometimes, or putting extra zeros other times, and the essential equivalence between these concepts, because of the above conventions. (only now are we getting onto the actual understanding of the procedure!)
- (When it comes to dividing by powers of 10) The convention of expressing numbers less than 1 as beginning with 0.x, as opposed to just .x
Now, I haven’t expressed these particularly well, but that’s partly my point. These are conventions and understandings that are so deeply embedded and so intuitively known by maths-experts that they are very difficult to explain well. In fact, I think they are nearly impossible to ‘explain’, in the sense of ‘here’s a 2-minute explanation on this convention that will give you everything you need to know!’ To the novice pupil, they seem so arbitrary at best, and contradictory at worse. It takes a very sophisticated understanding to differentiate between conventions 1 and 2, which are essentially telling you to do opposite things at opposite times. Sometimes we need to put an extra 0 in front of .36; other times we have to remove the extra zero in front of 036. Why? Well… give it your best shot explaining it if you think I’m wrong.

A lesson preview from TES – note, there’s nothing ‘simple’ about what’s happening. Firstly, where did those zeros come from? Secondly, where did the decimal come from? Thirdly, we never see numbers written like .8 – what’s going on?!
This stands in contrast to the popular view on ‘teaching for understanding‘, which is all the rage. Don’t get me wrong: I’m all for helping pupils understand. Yet in my view, topics that are more grammatical – topics that rely heavily upon subtleties of notations and conventions – are difficult to understand in the abstract. Either your explanation will over-simplify but then it won’t convey all that’s needed for understanding; or it will convey the full breadth of a topic but totally overwhelm most of your pupils.
It may help to define mathematical grammar. In my view, a grammatical topic is one where subtleties in convention and notation can lead to serious confusions and apparent contradictions, despite deep logic underlying those conventions and notations. This is exactly what we see in teaching multiplying and dividing by powers of 10. (For what it’s worth, I’m less interested in the ontological question of whether there is such a thing as mathematical grammar. My interest is focused on the extent that grammar is useful as a pedagogical concept in maths, for categorising certain topics and implying a best way to teach them.)
So, to link it back to English grammar: my pedagogical-functional definition of grammar shares similarities with the learning of English grammar. For example: these two examples of full stops, and the definitions given, seem to contradict:
1. to mark the end of a sentence that is a complete statement
2. to mark the end of a group of words that don’t form a conventional sentence, so as to emphasize a statement – ‘I keep reliving that moment. Over and over again.’
Of course, they don’t contradict. Yet I don’t think any primary English teacher will race to teach and explain usage number 2 whilst also teaching usage number 1. Similarly I remember learning these golden rules in year 3: never ever start a sentence with ‘and’ or ‘because’. And they were good rules at the time! (Irony intended). But after you’ve gotten to an age where you’ve read thousands of stories of increasingly sophisticated language, and received enough of the appropriate guidance, the two usages will begin to fall into place, and you’ll reach a level of understanding where using full stops is as natural as breathing.
So. The common issue with grammatical topics: just like the usage of full stops, they are easy to explain & understand poorly and very difficult to explain and understand comprehensively. There’s too much underlying logic that pulls in different directions. So, I’m increasingly convinced that with grammatical topics in maths, just as with language, understanding must follow grammatical fluency and familiarity. Our understanding of them requires a mass of examples, together with a mass of practice, cohering together, over a stretch of time. Now, I’m not saying that this is sufficient for understanding place value, but that it’s undoubtedly necessary for pupils who struggle with maths.
Let me illustrate this with some topics. Aside from × 100, here are some other topics which strike me as grammatical:
Rounding – a notoriously difficult subject to make stick – why does 0.446 to the nearest hundredth round to 0.45, whereas 446 to the nearest hundred rounds to 400? Why doesn’t the former become 0.450? Why doesn’t the latter become 4? These questions are hard to explain, and a good explanation doesn’t usually help pupils get it right! Again – some of the similar conventions we saw with × 100 play havoc with rounding.
Simplifying algebra – after all, the rules of simplification are like the grammar of another language! 3a + 2a = 5a, yet 3a × 2a = 6a²? A tiny change in notation (+ to a ×) leads to a radically different process; there’s a deep logic, but it’s hard for pupils initially to understand. Then there’s all the conventions of invisible multiplication signs. I think simplifying algebra is a particularly good example of a grammatical topic, since in my experience, pupils are absolutely fine within lessons, within each topic; yet when it comes to tests and mixed exercises, all manner of confusion erupts. Again, there’s a very deep and rigorous logic to these processes, but I’ve found it’s far more helpful to tell confused pupils initially ‘this is how you add terms, and this is how you multiply them – just remember the two processes’.
Rearranging equations: again, a topic that seems so natural to maths teachers, yet so alien to most pupils. At first there seems to be a clear logic (and of course, like all of algebra, the logic is rigorous and wonderful) you can teach – ‘look at the order of operations performed on the variable, then reverse them!’ (although even that is difficult for most). But then you try and build up to funky questions like this: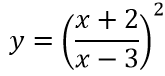 And then all explanations are off, and it’s basically just ‘okay, watch how I do it, now try five, learn this pattern…’
And then all explanations are off, and it’s basically just ‘okay, watch how I do it, now try five, learn this pattern…’
A great example of this is seen in this brilliant post on Math with Bad Drawings:
Simplifying algebraic fractions: 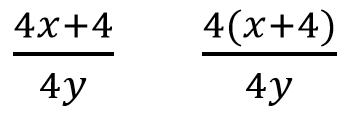
If you’ve tried it, you’ll know it’s a pretty difficult task to explain why you cancel both fours in the numerator of the first fraction, whereas you cancel only one four in the numerator of the second fraction. Of course there’s a deep logic, and there’s probably a decent paragraph length explanation – but I highly doubt any teacher tries to teach the patterns of simplification through an ‘explanation for understanding’. Again, a subtle difference in notation, and all of a sudden previously acquired heuristics are totally unsuccessful and highly misleading. As shown in how prevalent errors like these are:
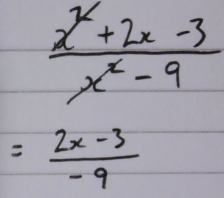
Negative numbers: I think this one goes without saying! I’ve written on it previously; I think this a prime candidate because of that fatal and poorly used heuristic: ‘if the signs are the same it’s +, if they’re different it’s -‘ – that falls into the grammatical trap of over-simplifying a topic and thence leading pupils astray.
So, onto the golden question: how should we best teach mathematical grammar?
1. Before teaching a topic, reflect on how ‘grammatical’ it is.
Recall my definition: can you explain the concept/method/process clearly and succinctly in such a way that covers all the eventualities and forestalls confusions with similar-looking processes? Teaching percentages of amounts: yes. The topics above? Not so much. Too many apparent-exceptions, strange conventions, surface similarities with different topics.
If a topic seems grammatical, break it down into every single possible strange case, as I did with the questions right at the start. The best way is to treat each case as a different thing to teach and practice explicitly. For example, in basic simplifying algebra, I’d want to split up 4a + 5a separately from 4a + a, and recognise they’re quite separate cases. After all, in my experience, when I’ve taught both problem types together before getting pupils to practise, a proportion of the class will inevitably get it wrong because ‘oh sir I forgot about the invisible coefficient of 1’; they’re familiar with the key concept, but they just weren’t familiar enough with it.
Furthermore, when you realise that a certain topic is particularly grammatical, plan to spend more time than you might normally assume is necessary. Remember, grammatical topics are particularly prone to the ‘curse of knowledge’ – experts find them so easy and logical and straightforward that we don’t realise how much time novices need to get proficient in them. We’re happy leaving a lot of time for trigonometry, for instance, but perhaps we don’t even spend any time in KS3 explicitly teaching multiplying by powers of 10. (One of the reasons I love teaching at Michaela is how so much time is given to these topics: I got to spend the best part of a month on base 10, and our year 8s have spent half a year on algebra without even reaching equations yet!)
2. Start slow, build up.
Compare how Daisy suggests teaching grammar:
I would begin with very simple and patterned sentences like ‘I walk to the shops’, ‘I eat lots of chocolate’ and get pupils to identify ALL of the parts of speech in them. I would start with the following five parts: verbs, nouns, adjectives, articles and prepositions, in that order…. If you look at the sheer amount of stuff that is necessary just for a basic understanding of a simple sentence, you will see firstly that you need to spend quite a lot of class time on this, and secondly that pupils will need to memorise a lot of the rules and processes.
Try and strike the tricky balance of nailing just one concept, but practicing it in an intelligent way that requires thinking which doesn’t conflict with the concept you’re trying to get across. (This is for numerous reasons: 1) two birds with one stone; 2) desirable difficulties help us learn; 3) non-conflicting difficulties can prevent boredom in doing the task.) For example, if I want my pupils to embed the idea that the decimal point in integers is invisible, and on the right of the number, a suitable set of questions might take the form of:
- 36 ÷ 10
- 482 ÷ 10
- 57643 ÷ 10
- 4382 ÷ 100
- 381 ÷ 100
- 67524 ÷ 1000
- 38925 ÷ 1000
There’s some thinking involved in the different divisors; but throughout, pupils are practising and internalising the invisible decimal point. Notice that at this point, I haven’t introduced the idea of filling in placeholder zeros; I want the focus to be entirely upon one key new concept. I might then make it a bit harder, interleave questions like so, to practice embedding the concept backwards and forwards i.e. the decimal point can be made invisible if it ends up on the right of an integer:
- 36 ÷ 10
- 4.8 × 10
- 482 ÷ 10
- 1.9 × 10
- 57643 ÷ 10
- 4382 ÷ 100
- 6.22 × 100
- 381 ÷ 100
- 6.44 × 100
- 67524 ÷ 1000
- 7.536 × 1000
- 38925 ÷ 1000
Once this is in place, move onto a different task, to embed a different concept, and leave this one temporarily behind. For example, I might move onto the idea of filling in placeholder zeros when decimal points are ‘moved’ beyond the visible number:
- 336.1 × 100 =
- 33.61 × 1000 =
- 24.7 × 100 =
- 1.91 × 1000 =
- 246.1 × 100 =
After they’ve got some fluency with this, mix the question types with the previously learnt process – and prepare for some confusion! E.g.
- 336.1 × 100 =
- 4.8 × 10
- 33.61 × 1000 =
- 3.26 × 100 =
- 24.7 × 100 =
- 7.536 × 1000 =
In my experience many hands will be raised – ‘sir do I have to fill in the zeros in question 2?’ to which a simple reassurance usually suffices: ‘no, this one was like the ones we did 15 minutes ago! Where should the point end up? Do we have empty cups that need filling? [‘No sir.’] Exactly.’
This might all take place in one lesson, or over week, depending on the class. But each time, follow these steps:
- Practice each new concept separately
- Gradually interleave with previously drilled concepts
- Move onto a new concept, and practice that separately;
- Gradually interleave with previously drilled concepts.
- Repeat!
3. Practice, practice, practice – over time.
Remember, the things they’re learning still seem to pull at odds, so over time, some of it will fade, and some of it will stick. As a result, if it all isn’t rigorously revisited, one pupil will be able to do 4.6 × 1000 = 4600, but then answer 4.6 ÷ 1000 = 0046, too.
A good way to revisit is to drill over time. Randomisable Excel spreadsheets are your friend here. Make it fun! Make it competitive! Time pupils and see if they can beat their class score. They will love their increasing success.
Here’s a drill I made just after my low-prior-attaining year 7s had gotten the hang of some basics of × 10. We practised this every day, or every other day, for a couple of weeks. Notice the different question types and all the different cases involved in multiplying and dividing by 10 – place value is really complex!
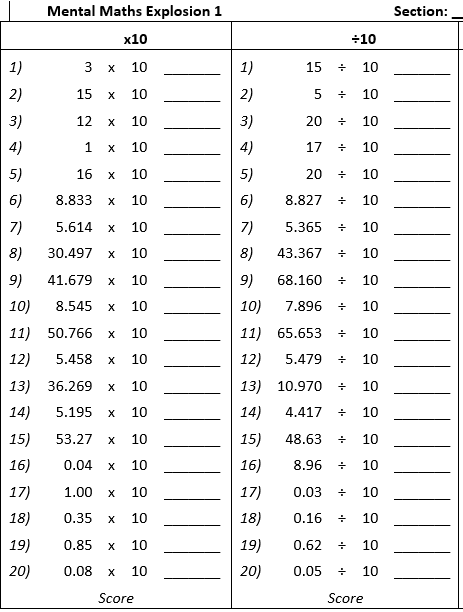
(Incidentally I love saying things like ‘GET YOUR EXPLOSIONS ON THE DESK!’ or ‘PUT YOUR EXPLOSIONS AWAY!’. I think the class enjoy it too.)
4. Prepare to fly
The great thing about getting it right with grammatical topics is that they are usually foundational to many other topics. And once pupils start getting mastery in the basics, their potential for growth is exponential. A nice illustration with the MENTAL MATHS EXPLOSION that those same year 7s, several months later, are currently doing:

It’s so much harder! But you quickly realise that once the foundations are firm, things like standard form, × 0.1, etc. are so easy to incorporate. In a future iteration of these Mental Maths Explosions I might spend 15 minutes of class time on multiplying by negative powers of 10, just to spice things up a bit – but since everything else is in place, they’ll be absolutely fine with that.
For what it’s worth, the first drill above was done in December, and we started this drill only three months later, in February – off the back of about 2 weeks’ explicit curriculum time, and 2 minutes a day thereafter. I was pleased to see that in our mid-term exams, one of the best answered questions by my class was the following:

Once the launch pad is in place, prepare for lift off.
_________________________________
Postscript: on moving the decimal point…
I’ve received numerous tweets and comments on how the decimal point doesn’t move. My wonderful boss (another great plus of working at Michaela!) has written a great reply to that point here. Interestingly, like her, I heard numerous times and saw numerous demonstrations in my PGCE year on how the decimal point doesn’t move. In fact I even copied wholesale a teaching approach I saw during one session: I printed out digits and a decimal point, 1 each on a piece of A4 paper, made pupils stand up, and slid them up and down whilst the decimal point stood the same. From that experience – and how it offered my pupils precisely zero benefit in learning any of the issues & conventions I discussed above – I quickly learnt never to spend time on it again. In my experience, the key roadblocks to success in this topic have nothing to do with whether the decimal point or the digits move; instead, they are all related to the highly confusing conventions I mentioned above, which stand regardless of whether you move the decimal points or the digits.
One might then argue that it’s best to teach ‘move the digits!’ because it’s true. My main response to that is that moving the decimal point is far easier and less cognitively overloading. That’s why numerate adults – even those who know that ‘the decimal point doesn’t move’ – nonetheless overwhelmingly move the decimal point when they are working out a divide by 1000 question.
But more related to teaching: many of my lowest-attaining pupils, the ones who struggle the most and who didn’t understand this topic at primary, have real trouble just moving the decimal point – their difficulties in spatial awareness makes them do things like this:

Can you imagine how difficult these pupils must find the concept of ‘keep the decimal point there, and move all the digits along!’ – so much is moving at the same time! Especially as there isn’t any working out that can help them, unlike the arrows for the decimal point. I’ve seen these pupils gain real confidence in moving the decimal point and I am loathe to give them a much harder, more cognitively demanding process that some of them will find far too difficult.
For what it’s worth, our textbook also makes clear the concept that the decimal point doesn’t really move. But on a procedural level, we stick with moving the decimal point all the way, as a handy shortcut.
But please do read Dani’s post for numerous extra explanations on why ‘the decimal point doesn’t actually move’ is not particularly helpful pedagogically.
If you enjoy this sort of thinking into maths pedagogy, you might enjoy working at Michaela! Contact me on Twitter [at]HinTai_Ting for more details.





“a notoriously difficult subject to make stick – why does 0.456 to the nearest hundredth round to 0.46, whereas 456 to the nearest hundred rounds to 400? ”
Surely it doesn’t. Rounding 456 to the nearest hundred is 500, or am I going insane? 400 is what you get if you round down to a multiple of 100.
LikeLiked by 1 person
glad someone else spotted this!
LikeLike
Thank you for spotting this! Edited.
LikeLike
The convention of writing 0.36 instead of .36 appears to be slipping away, incidentally. My TI-84 Plus CE takes it away, and I’ve been told that’s the New Way.
LikeLiked by 1 person
Interesting! Not sure if it’ll make understanding easier or harder. It’s nice to make explicit that 0.x numbers are less than 1 and greater than zero. But again, it’s an extra convention that needs to be picked up. As with many things, gains and losses come together.
LikeLike
My feeling is that, overall, it’s better to have it than not. The reason for the 0 that I remember being given when I was learning mathematics is that its presence minimizes confusion: Because we never write leading zeroes otherwise, 0. clearly reinforces that this is a decimal in [0, 1) (obviously, they didn’t put it in that notation when I was in elementary school 😉 ). But I’ve recently been thinking about language: We use “point” in secondary school mathematics in two apparently distinct ways: to indicate positions on a number line, Cartesian plane, or Cartesian 3-space, and to indicate that we’re now providing the non-integer portion of a number. What if those aren’t actually distinct ways? That is, what if using “point” for 3.56 emerged conceptually because we’re going to point #3 on the number line, then going a little bit further? Even if that’s not the history (which it likely isn’t), that could be a useful teaching tool. It does have the snag that we need to clarify that we’re starting at 0 and heading in an appropriate direction (3.56 is to the right of point 3, but -3.56 is to the left of point -3).
Removing it really just moves the goalposts a tick. We no longer have to explain why 0.356 has a leading zero, but now we have to explain why .0356 does. And regardless, we still have to explain why 3.56 * 1000 has a trailing zero (3560) but 3.56 * 100 doesn’t.
LikeLiked by 1 person
Another thought: In high school and college, my science class instructors were adamant that there’s a difference between 3, 3.0, and 3.00, and so on (specifically, 3 represents any value in [2.5, 3.5), 3.0 any value in [2.95, 3.05), etc.). In mathematics, we don’t care so much, but it’s an important part of the grammar of mathematics in science.
LikeLike
I’d say that talk of moving the decimal point (although it’s what many of *us* do quickly) is not helpful at all when you are first teaching this. When you multiply or divide by any power of ten the value of the digits change, so it’s the digits that move, the decimal point never moves.
LikeLiked by 1 person
Although let me point out that I’m not suggesting you don’t know this at all! Just adding something on the end as I come across loads of non-specialists in my job who genuinely don’t know this point. 🙂
LikeLiked by 1 person
like jemmaths I was going to stress the importance of stressing its the digits that move -NOT THE POINT! Indeed in primary maths teaching saying th point moves is regarded as almost as heretical as saying ‘you just add a zero’ when multiplying by 10. I think we should explain how the grammar works. I like to point out that the number 7(for example) could be written as 07 or 007 or 0000000000007 and would still be the same value – in fact it could have an infinite number of zeros to the left but that’s silly so we’ve all decided not to write them (‘trim that number’). of course some mechanical and digital devices still have them eg the 24 hour clock. Then introduce how in decimals the redundant zeros are on the right – again explaining why. Our 7 could be 7.0 or 7.00 or 7.0000000000000000000000 without it changing value (notwithstanding the comment about sicence above which was beyond me). Then children can sort necessary place holding zeros and unnecesary ‘head a hair cut’ zeros.
We teach x10 with the chant (and an associated set of actions) Multiply, go large, left. and /10 with divide. reduce, go right. Some local secondary school maths teachers came to visit and finally understood when a seemingly random selection of year 7’s would jump out of their seat, jump to the left (and make an X with their arms whenever they talked about x by 10. Then they realised that were all our alumni!
LikeLike
“(notwithstanding the comment about sicence above which was beyond me)”
Since science is about real world measurements, and real world measurements are only as exact as the tool being used to measure, the tradition (at least as I was taught) is to only provide as many digits as you can safely measure. If you say something is 1 m long, you’re saying you measured it with a meter stick and it was “close enough” to a meter. If you say something is 100 cm long, you’re saying you measured it with a ruler with centimeter marks and it was closer to 100 cm than to 99 cm or 101 cm. So 100 cm is a more precise measurement than 1 m is.
As far as mathematicians are concerned, 1 m = 100 cm, and 100.000001 cm is just as close to 100 cm as it is to 1 m.
Just as a scientist is more likely to say, “Pi equals 3.14, to two decimal places”, while a mathematician is more likely to say, “Pi is approximately 3.14”.
Hopefully this helps at least a little. 😀
LikeLike
Thanks- I understood that. Thank you for taking the time to explain.
LikeLike
I like a lot of the terms you use to describe redundant zeros! Terminology is so helpful.
Key question: would you ever teach them to move the point as a shortcut? Or would you force pupils not to do that when answering these questions? (I’ve also updated my postscript for some more reasons why we teach this way!)
LikeLike
Wary of the danger of being tarred as ‘holier than though’, I shall just link to Daniel Willingham’s piece on the danger of just doing the procedural knowledge without the conceptual understanding.
http://bit.ly/2mgikE9
And I agree that automaticity is important. And also that teachers should be teaching the understanding and just because one section/topic/concept is difficult does not seem a good enough reason to me to use something that they acknowledge is wrong, instead.
LikeLike
Interesting! that picked up an old wordpress name I have never used.
Tim Stirrup
LikeLike
I enjoyed that article, thanks for posting it.
LikeLike
Great article, thanks Tim. You seem to be advocating a both-and approach – would you teach the procedure of moving the decimal point at all? Or would you require pupils not to do that? (I’ve also updated my postscript for some more reasons why we teach this way!)
LikeLike
Pingback: Drill and Thrill | Until I Know Better
Simplifying algebraic expressions and changing the subject of a formula – there are concrete/pictorial models that help students to make sense of these (bar models, algebra tiles, model it as an area….). They work much better than just saying ‘do it like this’ .
LikeLike
I’d love to know how you use these to teach a question like this:
Make b the subject of the formula:
a = (c – bc)/b
LikeLike
Pingback: Is this the best we can do? Part 7: the spacing effect | mathagogy
Pingback: «اللغة التي كتب الله بها الكون».. لماذا تعتبر الرياضيات لغة حقيقية؟ 2021