Is this the best we can do? Part 7: the spacing effect

This is part of a series offering my views on some problems with and solutions for UK maths education. The first part looked at the state of affairs with regards to GCSE and PISA results, the second part looked at my attempt at a diagnosis, the third part looked at pre-existing maths education success stories, the fourth part looked at how textbooks offer the largest potential to improve pedagogy across the nation, the fifth part examined the role of hard work and homework, and the sixth part diagnosed the problem of forgetting in maths education. This part examines one solution to improving maths memory: employing the spacing effect.

I remember it well. I’d reached the end of my first ever half term of teaching. But standing between me and the holidays was a large pile of assessments to mark. At first, the prospect didn’t seem too bad: I thought it would be relatively mindless work. But that belief was before I actually started the marking itself. My dreams of a mindless few hours rapidly transmogrified into a nightmare: the nightmare of realising how poorly my classes had done. Question after question hit me with the same realisation: ‘we’ve covered this in class – we even looked at this yesterday, in our revision lesson – how on earth did you get this question this wrong?’

 

(scores are real, names have been changed)

The above table shows a representative sample of results from one class. Some pupils had turned in pretty good papers. But as a whole, across all my classes, the class average was pretty close to 50%. As a pupil myself, I could never have even comprehended getting 50% in a maths exam. As a teacher, I was even more baffled. I had taught 100% of the topics on the test – what on earth had happened to the other 50%?

Seeing my class results as a whole then pricked me with a deep fear. This was first half term as a teacher. What if I had been making some terrible mistake? What if I was a far worse teacher than I, or my tutors and mentors, had realised? With anxiety I found a fellow maths teacher in the staffroom and and told her of my predicament:

“So, my classes have done really poorly – I don’t understand what’s happened.”

“Oh no! What do you mean? How poorly did they do?”

“So, I think the class average is about… 50%? Most of them seem to be getting around 29 out of 55.”

“50%! Oh! DON’T worry about that, that’s fine! My classes get around that too.”

“Oh…. but how come they don’t get more? I taught it to them, after all.”

“They’ll pick it up later on. It’s fine!”

Thus ended my first half term as a teacher, and with it, my naive hopes of pupils remembering everything that I taught them.

Yet at the same time, it ignited within me a passion for maths pedagogy that eventually led to this blog. What if there is a better way than simply expecting so little from our teaching? What if there were some way of getting pupils to score close to 100% in tests? What if there were some way of getting pupils to remember nearly all of what you teach them?

Teaching mathematical grammar

Consider these questions:

1. 3361 × 100 = 336100
2. 3.361 × 100 = 336.1
3. 33.61 × 100 = 3361
4. 0.3361 × 100 = 33.61
5. 336.1 × 100 = 33610

To a maths teacher, or a pupil who achieved old-money KS2 level 5 in maths, these are utterly trivial questions that require barely any conscious thought.

Yet to any pupil who finds maths difficult, these questions can be bewildering.

On the surface they are all the same process – ×100 – yet the process performed on each number looks radically different. Take question 1: 3361 × 100. Simple, right? Put an extra two zeros at the end of the number, and it’s right. But apply that process to questions 2, 3, and 4, and you’ll get it totally wrong. Question 2: 3.361 × 100. Similarly simple: all you have to do is move the decimal place two places to the right . But in question 3, the decimal point has disappeared altogether in the answer – where’s it gone?! Then over to question 4 and 5, and two weird things happen: whilst the decimal points have moved as expected, a zero has disappeared from the left of the number, whereas in question 5, a zero has appeared on the right of the number.

To illustrate: have a look at these mistakes, and see if you can spot the inferences made:

1. If 3361 × 100 = 336100, then: 3.361 × 100 = 3.36100
2. If 33.61 × 100 = 3361, then 0.3361 × 100 = 03361
3. If 3.361 × 100 = 336.1, then 336.1 × 100 = 3361 .

Of course pupils find it bewildering.

I’ve started to think that this topic is a great example of mathematical grammar, and as such, requires a specific form of teaching for pupils to learn it well. What do I mean by this? And how can we help pupils get it?

Starting at Michaela

In September I started teaching at Michaela.

What drew me there? The first thing was Michaela’s mathagogy. Over the summer, I reflected on my experiences as a maths teacher in the series ‘Is this the best we can do? Doing better’, looking at issues with UK maths education such as work ethic, textbooks, pedagogy, subject knowledge, expectations, behaviour. Much of the inspiration from this series has come from Michaela teachers. (I didn’t quite write all the posts I was intending to write – but I’m hoping to finish off the series, especially in light of my experiences at Michaela, trying to put some of these into practise.) I’ve been eagerly following Michaela blogs since the school started, and found myself nodding along to(/exuberantly absorbing) many of their thoughts – for example, on recall, or the foundations of teaching problem solving; or teaching efficiency in strategies; or on making textbooks. So it felt like a natural fit.

And then I visited. Watching one of the maths team teach an hour of maths was one of the highlights of my year, and that one hour hugely transformed my own teaching practice when I returned to my previous school. (To list a few things, I started speaking much faster in lesson, expected 100% attention, encouraged pupils to take more responsibility for their results, heightened my own expectations, and showed my own personality more. All from watching her for an hour!) I knew I wanted to work there. More than that, I knew that I couldn’t bring about my thoughts on maths education all by myself – such as making textbooks, or setting daily homework, or regular testing – but Michaela seemed to be doing it all, and more, already.

Those things drew me to work there. I’ve been there for a month. How has it been? Here are some reflections.

Respect

‘Those who can, do. Those who can’t, teach.’

– George Bernard Shaw

‘Why on earth are you a teacher? I still don’t understand. You could’ve done so many things and you chose to become a teacher.’

– Multiple pupils

Respect in a profession is not the most important thing. Take rubbish collectors and lawyers, for example. Many jobs are not particularly respected – they may even be looked down upon – yet they nonetheless play an important part in society. They may even be relatively well compensated.

Nonetheless, respect is important. A respected profession is one which attracts high quality applicants. Given the teacher recruitment problems in the UK, it’s worth thinking about respect for the profession.

It’s also worth thinking about respect for the sake of well-being. Teachers are demotivated. While there are a huge variety of causes for this, a sense of general respect in teaching would undoubtedly help.

So, how respected are teachers?

Thoughts on ‘no excuses’ discipline

I attended the Michaela debate on Saturday 23^rd April. The debate on ‘No excuses discipline works’ had me thinking the most, with the barrister-esque Jonathan Porter speaking against the wise and fatherly John Tomsett. It was a brilliant debate. They have both since posted their transcripts online, and other prominent bloggers who were present have offered their responses; this has in turn produced a lot of reaction from people not present for the debates.

All this has shown sharp divisions in the first order debate: people’s opinions and interpretations of ‘no excuses’ discipline and what it means. Yet it’s clear from the sharp divide that there are serious second order issues: what a behaviour system is for, and what values ought to underpin it.

It’s increasingly clear that big ethical questions pervade and underlie this entire discussion. For example, both sides grapple with the idea of fairness:

Reverse explanations: focusing attention on what’s new

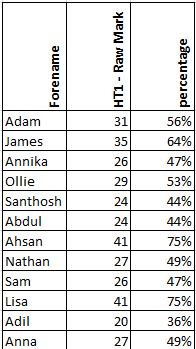
So, you’re convinced of the worked example effect, and you use it in lessons with great regularity and regular success. Yet have you ever worked through an example only for your students to be completely flabbergasted?

This happened to me the first time I taught quadratic simultaneous equations to my year 11s (set 2/4). They were pretty solid in solving quadratics and at simultaneous equations by elimination – we’d just spent half the lesson revising them. I put this example up on the screen:

and I duly worked through it, rearranging 2, substituting into 1, reminding them of how to expand a binomial squared, expanding and simplifying and solving and then finally substituting again. In fairness I should have stopped much earlier, from the puzzled sounds that were emanating from the class. But it soon became clear from questioning that students had absolutely no idea what had just happened. The problem: total cognitive overload. Whoops! I tried to start again, emphasising each step, but I had lost most of the class’s motivation, and we duly went back to revising quadratics and simultaneous equations.

Fast forward a term (I hoped that was enough time for them to recover from my first attempt). Same class, same topic – yet very different approach. I didn’t start with the problem, or work through an example. Instead, I tackled through the problem in reverse. Again, the starter was a mix of quadratic equations of varying complexity. But after we’d revised that, this was my sequence of examples, in this order:

Slide 1

This was the first slide – and it was very easy compared to lots of the questions in our starter. I picked a student to solve it for the class, and she quickly did.

Slide 2

This was slightly more complicated, but again within the reach of the class. I again picked a student, asking what was different, and then asking them to solve it. However, upon rearranging, many students immediately recognised that it led to the same problem as before, and so we already knew the solutions.

Slide 3

Slide 3 – a great way to highlight some misconceptions – I picked a mid-attaining student from the class who correctly identified the first step as expand the brackets, but incorrectly stated it as the classic ‘x squared plus 4’. Students discussed this briefly (whilst I went mock-apoplectic at him), and thankfully other students quickly corrected him. After that pause, we simplified and saw – it was exactly the same as the problems in the previous slides, and again we knew the answers. And then finally:

Slide 4

Quadratic simultaneous equations – finally, our new bit of learning. I introduced the concept of expression substitution to them, and showed how it worked, and the resulting equation that formed. And once again, to no-one’s surprise by this stage, we were led to exactly the same equation that we had had in the previous slide. As a result, the rest of the process was trivial – I simply told them to ‘solve the remaining equation as we just did’, flicked back each slide (where we’d solved each problem on the board), and students knew exactly what I meant. I then immediately went back to the first slide, and the solution we’d arrived at there, and asked if that was the final answer. Impressively, a large number of students were able to immediately identify that we had to solve for y as well. It was clear that this method of explaining in reverse had avoided the catastrophic working memory overload of my first attempt. And, when it came to trying problems, the entire class (ranging from predicted grades of Cs to A*s) were able to solve at least several problems successfully.

These two experiences couldn’t have been more different. The only difference was the un-intuitive – but highly successful – reverse ordering of my explanation. Like many good ideas, I originally encountered this from Kris Boulton, who used it in the context of linear simultaneous equations; I’m blogging about it just because I haven’t seen it mentioned anywhere else, but it’s been massively helpful to me in this instance and several others, and I’ve wished I’d used it more in other topics.

I think the key pedagogical insights of this method is as follows:

1. In worked examples, focus attention and cognitive load, as far as possible, on the new concepts/processes/facts that you want pupils to learn. 
2. Recognise that if a worked example contains parts that pupils are already familiar with, it nonetheless contributes to cognitive load, and thus may hinder their ability to grasp what’s new.
3. Therefore, if a worked example involves steps that utilise lots of other previously-learnt things, work through the problem in reverse, establishing the most basic steps before you move onto what’s new.

In the example above, the new concept was of substituting between equations, and the rest of the example reduced to things that pupils already knew how to do. Yet as my first experience showed, those parts of the example involving rearrangement/simplifying/solving quadratics overloaded my pupils, who were undoubtedly still trying to get to grips with the idea of equation substitution. As my second experience showed, far better to start with what they felt comfortable with, establish it (and in the case of (x+2)^2, get the peripheal & familiar misconceptions out of the way there), and work backwards until we reached what was new.

This method can be used in pretty much any topic which involves multiple steps. It can work in KS3 – for example, when teaching ordering fractions, decimals and percentages:

First example/problem: Convert 1/2, 1/4, 3/10 into decimals

Second problem: ‘Order 0.6, 0.2, 0.5, 0.25, 0.62 in ascending order.’

Worked example: ‘Order 3/10, 0.2, 1/2, 1/4, 0.62 in ascending order.’

A similar principle also works in KS5 teaching too, especially well, as most questions are rather long. Since questions here have numerous parts and it’s a bit harder to separate them out, I often apply a slightly different but related approach: pre-provide everything that the students already know how to do in the example, so that they can focus on the new content.

For example, the Edexcel C2 textbook offers something like this example for binomial expansion approximations: ‘Find the first four terms of (1+8x)^6, and by using a suitable substitution, use your result to find an approximate value to (1.016)^6.’ Yet the only thing that’s new is the last bit – approximations using substitutions. So, when I explained this new process, I simplified the example by providing the familiar part of it for them: ‘The first four terms of (1+8x)^6 are 1 + 48x + 960 x^2 + 10240 x^3. By using these and a suitable substitution, use your result to find an approximate value to (1.016)^6′.

By pre-providing the first part of the answer within the example, we instantly honed in on the new content, directed all our attention to that, had lots of time to ask questions about it, and weren’t held up by having to perform the expansion. Interestingly, when students eventually did see an exam-style question, they twigged by themselves the need to expand it first, and happily did so. Similarly, with my year 11s and the simultaneous quadratics, most of the class worked out for later questions (with a bit of discussion with their partner) that they had to rearrange some equations before substituting them. I think this happened because, having been able to focus entirely on the new process during the reverse explanation, the students had already grown quite comfortable with it, and were thus able to apply other parts of their prior knowledge to new and harder questions without much further instruction from me.

 

 

We naturally want to introduce what’s new first. Yet if this is then followed by lots of other familiar content in order to get to the final answer, we run the risk of cognitive overload in our pupils. As teachers who have mastered the curriculum, this often doesn’t occur to us, so I’m thankful for that original lesson with my year 11s for bringing this strategy back to mind. Either reverse your explanations so more familiar final steps are addressed first, or just pre-provide the familiar steps of an example, so that you can focus pupils’ attention and working memory on what’s new.

Variation theory applied: peripheral questions

We felt very nice and snug, the more so since it was so chilly out of doors; indeed out of bed-clothes too, seeing that there was no fire in the room. The more so, I say, because truly to enjoy bodily warmth, some small part of you must be cold, for there is no quality in this world that is not what it is merely by contrast. Nothing exists in itself.

– Herman Melville, Moby Dick

Variation theory: you can’t fully understand a concept, unless you understand what it is not.There are loads of brilliant applications of this in teaching. Kris Boulton first introduced the concept to me via GCSE students who were unable to identify this shape as a pentagon:

The reason? While they might have been told that a pentagon is a shape with 5 sides, what they usually see accompanying this explanation is:

and it’s this regular pentagon that sticks in their minds as a ‘pentagon’, leaving them at a loss when faced with naming the unfamiliar shape above.

So, when defining the concept of a pentagon, it’s most helpful to show numerous examples of various irregular pentagons, together with shapes which are not pentagons, so learners can develop a full concept of what ‘having 5 sides’ means and doesn’t mean. It’s another way of addressing the problem Greg Ashman highlights here:

To experts, it’s obvious that the shape above is a pentagon, due to a thorough understanding of pentagons through many experiences; yet to communicate only that “a pentagon is ‘a shape with 5 sides’ that looks like ⬠” means that many learners will link the concept only with what’s been highlighted – the regular pentagon.

In this post I’ll look at one easy way to apply variation theory in designing tasks: adding peripheral questions to tasks.

Closing the gap: differentiation by time

There’s a lot of talk about differentiation by outcome, differentiation of explanations, differentiation of support, differentiation of task, etc. etc. etc.. Heck, there’s eighty purported differentiation strategies here.

I worry sometimes about doing differentiation for its own sake. We don’t talk so much about the goals or the assumptions behind differentiation, when those, to me, seem to be the much bigger questions. In this post I’ll explore some of those questions, and present my view of the conditions when, and how, differentiation makes sense. (The title gives you a hint.)

I remember watching this episode from the Simpsons on BBC2 when I was at school myself. This particular section has lingered in my mind since then, and since becoming a teacher it naturally came back to mind. As I watched it again, it’s even more devastating than I remembered.

While that clip has so much worth commenting on, Bart’s quote says it all:

“Let me get this straight. We’re behind the rest of our class and we’re going to catch up to them by going slower than they are?”

Differentiation via a slower remedial class: clearly a ridiculous idea – or is it?

The descriptive principle that learners minimize their cognitive load

I’ve written before on the normative principles behind minimizing cognitive load – i.e. to what extent should teachers design teaching so that learners’ cognitive load is minimized? This post, however, will focus on something foundational I’ve observed, that’s been in the background of these previous posts.

In my previous post I described the phenomenon where:

students are able to accurately reproduce a process, while being simultaneously completely unaware of the WHAT they are doing.

Similarly, the conclusion of another post was:

to enable students to learn x, I believe we should include desirable difficulties in tasks to ensure that students are required to use everything they need to know about x in order to solve the task; students are thus forced to think about everything they’re meant to be think about to understand x correctly, and they thus embed those thoughts.

I believe the underlying principle that explains these two recommendations is the following descriptive observation: whilst listening to instruction and doing tasks, learners aim to achieve ‘success’ while experiencing as little cognitive load as possible. This often has negative learning consequences and must be counteracted.

Someone else who’s noticed this phenomenon.

Here are some examples and suggestions related to this observation:

Germane load: linking processes with their names

Bokhove had some great comments on my post on minimizing cognitive load vs. desirable difficulties which clarified the debate for me. As he says,

Squaring [the circle of minimizing load vs. desirable difficulties] is not necessary.
Cognitive Load Theory does not state that less load=best… it should be about successful integration into schemas.
This fits in with all kinds of worthwhile processes Didau set out in his blog on fading, scaffolding etc. One mechanism can also be ‘desirable difficulties’ or intentional crises (perturbations, cognitive conflicts, productive failure). Yes they might (intentionally) spark load but they are conducive to schema building. (Emphases mine)

The phrase of ‘germane load’ stands out to me. It was emphasized again in this great blog post, which goes into much more detail:

encouraging learners to engage in conscious cognitive processing that is directly relevant to the construction of schemas benefits learning. For example, varying the conditions of practice appears to have beneficial effects upon learning, despite the fact that the presence of that variety would raise the loading on working memory. They called this germane cognitive load.

Since then post I’ve been thinking a lot about such day-to-day teaching strategies that might be conducive to sparking germane load: i.e. strategies which build students’ mathematical schemas. Hopefully there’ll be more such ideas in this series.

I’m sure I’m not alone in seeing this phenomenon: encountering a student(/whole classes) struggle with a starter question that was literally done yesterday, even when the whole class were getting it 100% right yesterday.

As many have said, evidence of a student performing a process accurately does not imply they’ve learnt it securely. Performance and learning just aren’t the same. Memory is crucial too.

Due to the fact we did it just yesterday, I think it’s more complex than a memory problem. Sometimes the problem starts even whilst students were getting all the questions right. From some of my observations, sometimes the problem is that students are able to accurately reproduce a process, while being simultaneously completely unaware of the WHAT they are doing.

Let me be clearer: here I’m not even talking about ‘understanding’ what they’re doing. What I mean is, students can be thinking deeply ‘so I multiply this number here with this one, then I add these ones all up, then I divide that by this total… let’s check if I have the same as my partner – yes! Great, I’m doing it right!’ And yet, all the while, they have no trace of the thought ‘I am currently finding the mean from a frequency table’.

This happened for some of my students in a recent lesson. Their pages were filled with ticks, yet when I was asking them ‘so what is this number? What have you just found?’, such students had absolutely no idea. It’s no surprise, then, when it comes to next lesson’s question asking them to ‘find the mean’, they’ve forgotten what to do. They never thought of it as finding the mean in the first place. In the terms used in the literature, they were failing to even begin building a schema; they were simply replicating a process, detached from any sense of what it was for.

I decided to blog on this as it seemed such an obvious and yet subtle issue with my pedagogy. And a problem that’s so easily correctable as well.

Next time round, I taught finding both the mean and the mode from frequency tables in one go; then the questions required them to find both measures from each. The students were then forced explicitly to label their answers: ‘mean = ….’ and ‘mode = ….’; they thus had to link the process of finding the mean with its name.

This solution can be used where there’s another similar easy-to-do process that can be lumped alongside the other process you’re trying to teach. I mentioned a very similar one in my previous post on finding areas and perimeters together in the same task. I think one could do similar things with fraction operations, angle facts, index laws, other statistics, and undoubtedly many other topics.

I do have some slight reservations with this strategy, however, due to it violating the principle of ‘separating minimally different concepts’. But from what I’ve seen so far, it’s worked better for medium/long-term retention than whatever I did before.

Undoubtedly there are other ways of linking processes with their names. I think this principle might lend itself usefully to plenaries too: e.g. a 1-minute ‘discuss with your partner: what have we learnt to do today? So, how do I find the MEAN and the MODE from a frequency table?’

I’m also a big fan of rhymes and chants as memory aids, and I think these have an even more powerful effect than simply lumping several processes together. I also think testing students on knowledge organisers might be the best way to do this in general (give them and expect them to learn the exact schema you want them to have in their mind!). However, effective memory aids and knowledge organisers take some careful thought and energy. When it comes to daily lesson planning in a sequence of work, lumping together several similar processes together is relatively easier to implement.

To bring it back to my original post, this strategy undoubtedly increases cognitive load, yet in a way that encourages schema-building. It seems to be working well so far.