Is this the best we can do? Part 7: the spacing effect

This is part of a series offering my views on some problems with and solutions for UK maths education. The first part looked at the state of affairs with regards to GCSE and PISA results, the second part looked at my attempt at a diagnosis, the third part looked at pre-existing maths education success stories, the fourth part looked at how textbooks offer the largest potential to improve pedagogy across the nation, the fifth part examined the role of hard work and homework, and the sixth part diagnosed the problem of forgetting in maths education. This part examines one solution to improving maths memory: employing the spacing effect.

I remember it well. I’d reached the end of my first ever half term of teaching. But standing between me and the holidays was a large pile of assessments to mark. At first, the prospect didn’t seem too bad: I thought it would be relatively mindless work. But that belief was before I actually started the marking itself. My dreams of a mindless few hours rapidly transmogrified into a nightmare: the nightmare of realising how poorly my classes had done. Question after question hit me with the same realisation: ‘we’ve covered this in class – we even looked at this yesterday, in our revision lesson – how on earth did you get this question this wrong?’

 

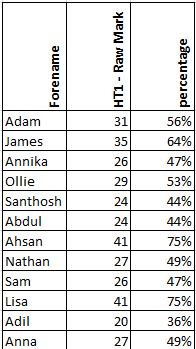
(scores are real, names have been changed)

The above table shows a representative sample of results from one class. Some pupils had turned in pretty good papers. But as a whole, across all my classes, the class average was pretty close to 50%. As a pupil myself, I could never have even comprehended getting 50% in a maths exam. As a teacher, I was even more baffled. I had taught 100% of the topics on the test – what on earth had happened to the other 50%?

Seeing my class results as a whole then pricked me with a deep fear. This was first half term as a teacher. What if I had been making some terrible mistake? What if I was a far worse teacher than I, or my tutors and mentors, had realised? With anxiety I found a fellow maths teacher in the staffroom and and told her of my predicament:

“So, my classes have done really poorly – I don’t understand what’s happened.”

“Oh no! What do you mean? How poorly did they do?”

“So, I think the class average is about… 50%? Most of them seem to be getting around 29 out of 55.”

“50%! Oh! DON’T worry about that, that’s fine! My classes get around that too.”

“Oh…. but how come they don’t get more? I taught it to them, after all.”

“They’ll pick it up later on. It’s fine!”

Thus ended my first half term as a teacher, and with it, my naive hopes of pupils remembering everything that I taught them.

Yet at the same time, it ignited within me a passion for maths pedagogy that eventually led to this blog. What if there is a better way than simply expecting so little from our teaching? What if there were some way of getting pupils to score close to 100% in tests? What if there were some way of getting pupils to remember nearly all of what you teach them?

Is this the best we can do? Part 6: the problem of forgetting

“If you wish to forget anything on the spot, make a note that this thing is to be remembered.”

– Edgar Allen Poe

“The palest ink is better than the best memory.”

– Chinese proverb

This is part of a series offering my views on some problems with UK maths education. The first part looked at the state of affairs with regards to GCSE and PISA results, the second part looked at my attempt at a diagnosis, the third part looked at pre-existing maths education success stories, the fourth part looked at how textbooks offer the largest potential to improve pedagogy across the nation, and the fifth part examined the role of hard work and homework. This part looks at the problem of memory in maths education.

The Persistence of Memory – Salvador Dali

In my career as a maths teacher, I flip regularly between deep job satisfaction and mild  despair.

Don’t get me wrong – I absolutely love my job. Most maths lessons I’m teaching pupils some sort of mathematical process. Most of the time pupils then perform that process with aplomb. Whiteboards with correct answers go up, I’m happy, the pupils are happy, I go around and mop up the remaining few pupils who weren’t quite 100%, put up some answers, and by the end of the lesson I and my pupils are feeling pretty pleased with ourselves.

But then comes the test. Even if it’s literally a few days later, and even if pupils face literally identical questions, their answers end up containing every confusion & misconception under the sun.

Whilst marking tests, I’ve often felt like Sisyphus – the mythical Greek figure condemned to roll a boulder up a mountain, watch it roll back down, and repeat forever. We strain and push our pupils up a mountain of mathematical understanding on a particular topic. After hours preparing pedagogy & teaching materials, then 60 minutes of communal graft in the lesson itself, it feels like we might have gotten somewhere with that topic. Then… fast-forward to tomorrow / the next week / the assessment, and those same pupils will literally deny having even heard of that topic before. ‘Gradient? What’s gradient?’

Yet I can’t write this solely as a complaint. After all, throughout my career, pupils have usually followed what I have told them. Lessons have gone well. I’ve explained things; pupils (seem to!) “get it”  and show they can do what I just modelled for them; we move on. So, if pupils are doing what I teach them, their forgetfulness must partly stem from a defect in my teaching. (Of course, I’m written previously on how hard work and homework plays a huge role in maths learning, so I can’t take sole responsibility for this failing: I constantly talk about the importance of independent revision, and many of my most forgetful pupils are those who give in shoddy, low-effort homework and never revise.) Nonetheless, there must be more that I can do.

The problem in a nutshell? I can’t think of a better way to put it than in Bodil’s phrase: ‘a lesson is the wrong unit of time‘. Much of our UK educational culture is focused on lessons: lesson objectives, lesson grading, showing progress within a lesson. As a result, we plan topics in lesson-sized chunks (‘addition this lesson, subtraction next lesson’), and we judge our success in lesson-sized chunks (‘the exit tickets show me they all learnt how to answer the key question this lesson’). But if we’re solely focused on lessons, then of course very little gets retained beyond that. Of course pupils forget. After all, as teachers, all we usually aim and plan for is for the pupils to ‘get it’ in the hour itself. To put the problem in reverse: we don’t teach with an eye for long-term memory; therefore pupils naturally don’t remember over the long term.

How big is this problem? And what can we do about it?

Teaching mathematical grammar

Consider these questions:

1. 3361 × 100 = 336100
2. 3.361 × 100 = 336.1
3. 33.61 × 100 = 3361
4. 0.3361 × 100 = 33.61
5. 336.1 × 100 = 33610

To a maths teacher, or a pupil who achieved old-money KS2 level 5 in maths, these are utterly trivial questions that require barely any conscious thought.

Yet to any pupil who finds maths difficult, these questions can be bewildering.

On the surface they are all the same process – ×100 – yet the process performed on each number looks radically different. Take question 1: 3361 × 100. Simple, right? Put an extra two zeros at the end of the number, and it’s right. But apply that process to questions 2, 3, and 4, and you’ll get it totally wrong. Question 2: 3.361 × 100. Similarly simple: all you have to do is move the decimal place two places to the right . But in question 3, the decimal point has disappeared altogether in the answer – where’s it gone?! Then over to question 4 and 5, and two weird things happen: whilst the decimal points have moved as expected, a zero has disappeared from the left of the number, whereas in question 5, a zero has appeared on the right of the number.

To illustrate: have a look at these mistakes, and see if you can spot the inferences made:

1. If 3361 × 100 = 336100, then: 3.361 × 100 = 3.36100
2. If 33.61 × 100 = 3361, then 0.3361 × 100 = 03361
3. If 3.361 × 100 = 336.1, then 336.1 × 100 = 3361 .

Of course pupils find it bewildering.

I’ve started to think that this topic is a great example of mathematical grammar, and as such, requires a specific form of teaching for pupils to learn it well. What do I mean by this? And how can we help pupils get it?

Starting at Michaela

In September I started teaching at Michaela.

What drew me there? The first thing was Michaela’s mathagogy. Over the summer, I reflected on my experiences as a maths teacher in the series ‘Is this the best we can do? Doing better’, looking at issues with UK maths education such as work ethic, textbooks, pedagogy, subject knowledge, expectations, behaviour. Much of the inspiration from this series has come from Michaela teachers. (I didn’t quite write all the posts I was intending to write – but I’m hoping to finish off the series, especially in light of my experiences at Michaela, trying to put some of these into practise.) I’ve been eagerly following Michaela blogs since the school started, and found myself nodding along to(/exuberantly absorbing) many of their thoughts – for example, on recall, or the foundations of teaching problem solving; or teaching efficiency in strategies; or on making textbooks. So it felt like a natural fit.

And then I visited. Watching one of the maths team teach an hour of maths was one of the highlights of my year, and that one hour hugely transformed my own teaching practice when I returned to my previous school. (To list a few things, I started speaking much faster in lesson, expected 100% attention, encouraged pupils to take more responsibility for their results, heightened my own expectations, and showed my own personality more. All from watching her for an hour!) I knew I wanted to work there. More than that, I knew that I couldn’t bring about my thoughts on maths education all by myself – such as making textbooks, or setting daily homework, or regular testing – but Michaela seemed to be doing it all, and more, already.

Those things drew me to work there. I’ve been there for a month. How has it been? Here are some reflections.

Is this the best we can do? Part 5: hard work & homework

“No food without blood and sweat.”

“Farmers are busy; farmers are busy; if farmers weren’t busy, where would grain to get through the winter come from?”

“In winter, the lazy man freezes to death.”

“Don’t depend on heaven for food, but on your own two hands carrying the load.”

“Useless to ask about the crops, it all depends on hard work and fertilizer.”

“If a man works hard, the land will not be lazy.”

“No one who can rise before dawn three hundred sixty days a year fails to make his family rich.”

– Chinese proverbs quoted by rice paddy farmers, from Gladwell’s Outliers

This is part of a series offering my views on some problems with UK maths education. The first part looked at the state of affairs with regards to GCSE and PISA results, the second part looked at my attempt at a diagnosis, the third part looked at pre-existing maths education success stories, and the fourth part looked at how textbooks offer the largest potential to improve pedagogy across the nation. This post will look at the role of hard work.

Malcolm Gladwell’s Outliers is a great read. Chapter 8, on ‘Rice Paddies and Math Tests’ should be compulsory reading for maths teachers: Gladwell sets out to answer that perennial question: why are East Asians so good at maths? Even when they have grown up abroad? The following chart, from a UK Education Committee report is absolutely staggering (though it looks at educational attainment more generally, rather than just maths):

Take a look at the topmost teal line: that represents the average grade of Chinese students in the UK according to their wealth levels. As you’d expect, it has a similar trend to every other line – Chinese students who come from richer backgrounds tend to do better than those from poorer backgrounds. But now compare the lines: The most deprived 10% of Chinese students in the UK outperform the richest 10% of every single other ethnic group, save for Indians. That is staggering.

Gladwell quickly and rightly disputes the claim that Asians have higher IQs – instead, he even cites James Flynn’s research claiming that ‘Asians’ IQ… have historically been slightly lower than whites’ IQs, meaning that their dominance in math has been in spite of their IQ, not because of it‘. Yet the fact that East Asians transplant their educational success even outside of their native countries means that the answer isn’t totally located in specific education systems, either: since it isn’t genetic, it must be something cultural.

So what else can explain this dominance?

Is this the best we can do? Part 4: better pedagogy through better textbooks

The demand for quality texts has been a cornerstone of the Escalante Math Program. In the seventies I realized that my students would be held back forever unless they had superior textbooks, so I searched for the best and tested many different texts. When I found what I needed, I demanded these texts for my students.

– Jaime Escalante (‘the most famous teacher in America’)

This is part of a series offering my views on some problems with UK maths education. The first part looked at the state of affairs with regards to GCSE and PISA results, the second part looked at my attempt at a diagnosis, the third part looked at pre-existing maths education success stories. This post looks at the first common theme in those success stories: textbooks. 

In 1982, two years before Singapore’s 16th-place ranking in TIMMS. the Ministry of Education published and rolled-out a new, intensely researched & resourced maths program.What did it involve? Research-driven textbooks, a prescriptive national curriculum, and mandated methods of instruction across primary schools in Singapore. 13 years later, Singapore jumps 15 places in the TIMMS rankings. The curriculum and the textbooks continue to be revamped, and Singapore’s scores keep on improving.

The dominance of ‘Singapore Maths’ should be well known to all UK teachers: in this last year, it has reared its head on our shores and even onto national news. So, there is a massive change in educational outcomes following a different curriculum and high-quality prescribed textbooks.

It’s a very similar story in Shanghai. Teachers across the city use the same expertly-created textbooks:

Shanghai mathematics teaching is based upon high-quality teacher resources. All schools follow the same textbook, which is published by the Shanghai education commission and refined and revised on an annual basis. Compare this with English schools, where, according to the TIMMS international survey, only 10% of mathematics teachers used textbooks as a basis for their teaching.

Interestingly, their textbooks are what you might call crowd-sourced; as Tim Oates writes in his brilliant paper on textbooks, they ‘are based on accumulated theory in maths education, are written and edited by expert authors, and constantly are supplemented by ‘adjustments’ from teacher-research groups. These teacher-research groups exist across the school system. Competitions are held, whereby ‘top’ adjustments are routinely fed through into the texts.’ What a great idea, and one for us to think about as well.

It’s a very similar story with Jaime Escalante, as his own words quoted above show; he spent a huge time comparing textbooks (which he describes as the ‘cornerstone‘ of his program), demanding the money for them. Moreover, where he felt they weren’t good enough, he supplemented them and even started making his own.

From these successes, I believe textbooks are the best answer to the crippling problem of when students ‘don’t get it’, the second signature problem I identified in my last post. As I see it, this problem has two interlinked causes: students have problems understanding because of missing mathematical foundations, and students have problems understanding because we little coherent nor specific ideas of the best methods for teaching each topic in maths. And the root of these causes is the fact that we maths teachers in the UK don’t have the best maths pedagogy at our fingertips, in a a readily accessible and classroom friendly way.

So, how can mere textbooks make such a crucial difference?

Is this the best we can do? Part 3: success stories

There isn’t a problem in teaching or learning that someone somewhere hasn’t solved. We just need to find them and take some field notes.

– Doug Lemov

This is part of a series offering my opinion on some problems with UK maths education. The first part looked at the state of affairs with regards to GCSE and PISA results, and the second part looked at my attempt at a diagnosis. This post addresses where to find potential solutions. 

Adam Creen responded to my first two posts in this series with this correct observation:

@HinTai_Ting thanks. If it was an easily solvable problem, we'd have cracked it years ago. But agree we shouldn't stop trying.

— Adam Creen (@adamcreen) August 3, 2016

This is true. After all, many agreed with my diagnosis and could identify with my experiences, but no-one offered any solutions. If the problem is widely recognized but there’s no readily acknowledged solution, then any solution must not be straightforward.

But: it doesn’t mean that no solutions exist. In fact, I’m optimistic they are out there. Why?

When I heard Doug Lemov of Teach Like a Champion speak briefly on his work, my abiding memory is of his deeply insightful focus: ‘there isn’t a problem in teaching or learning that someone somewhere hasn’t solved. We just need to find them and take some field notes.’

So, in Lemov’s spirit, this post will begin investigate: what education regions/systems/schools seem to have solved these problems with maths education? Following posts will then address: how do they do it? Do they address the UK-specific issues I identified in part 2? And how can we transfer these lessons to the UK, to our schools, to our classrooms?

Is this the best we can do? Part 2: Diagnosis

‘A correct diagnosis is three-fourths the remedy.’

– Gandhi

This is the second post in a series. In Part 1, I reflected on the vast numbers of 16 year olds who finish 11 years of maths education unable to answer the straightforward questions needed for a grade C. I argued that this is and continues to be a problem, despite rising C-grade pass rates over the past 20 years. This post reflects more deeply on the causes behind why so many 16 year olds are in this state.

Matthew Syed’s ‘Black Box Thinking’ is a great read. He examines extraordinary successes in various fields like medicine, healthcare, aviation safety – like Team Sky, or Google – to find what they have in common. The answer? Such successes ‘harness the power of failure’. They don’t shy away from mistakes, but rather expect them, learn from them, and milk them for all the information they are worth. The aviation industry does this extremely well:

Pilots are generally open and honest about their own mistakes (crash-landings, near misses). The industry has powerful, independent bodies designed to investigate crashes. Failure is not regarded as an indictment of the specific pilot who messes up, but a precious learning opportunity for all pilots, all airlines and all regulators.

Some examples from Syed that bear this culture out: flight accidents are automatically transferred to independent investigators to look into, and those involved in the flight are protected to full disclosure, as whatever they say is inadmissible in court. The report is then circulated and freely available to any pilot in the entire world, ensuring that the entire industry can learn from the accident. (This is a striking comparison to the education sector in this country– but that would require another blogpost in itself…)

As Syed goes on to explain, this culture is particularly useful since the dissemination and circulation of information on failures can quickly reveal ‘signatures’ – particular patterns that keep recurring in various mistakes, problems, and accidents. For example, in one week in 2005, a whole host of reports of near-misses came from pilots landing in Lexington Airport. The investigators quickly cottoned onto the problem from the info from the pilots’ reports: lights had just been installed on an adjacent plot of land, which was then being mistaken for the runway. Within days (apparently, quite slow for the industry – the adjacent land didn’t belong to the airport) the confusing lights were taken down.

In the spirit of this ‘black box thinking’, I’ve thought about what problems and mistakes I frequently observe in my own classroom, together with the mistakes and honest frustrations I hear from colleagues across various schools. I’ve focused particularly on my experience with bottom sets, since it is these groups that usually fail to make grade C (though my conclusions may be more widely true too). From the mistakes with these classes, what are the ‘signatures’ – the common recurring patterns? What are the issues I keep experiencing and hearing about from other teachers? And, in the following post – what way forward can be discerned from these signatures, from these diagnoses?

Is this the best we can do? Part 1: the problem

In 2014, 62.4% of teenagers sitting GCSE maths achieved at least a grade C – the ‘gold standard’ grade needed to progress onto a wide range of further study and employment. For the last 5 years, the pass rate has hovered around 60%.

The flipside of this statistic: every year, at least 40% – that’s a quarter of a million 16-year olds – complete their secondary education without having attained a C in GCSE maths. 

Is this the best we can do? 

I looked at the 2014 GCSE Higher maths papers. To have gotten a grade C in it, you needed 57 marks out of 200 (a statistic that shocked me when I first discovered it, and continues to shock). Below are 63 marks’ worth of questions from 2014’s two papers (click to enlarge) – if you got all of these questions right, give or take 2-3 of them, you would’ve done enough to get that coveted grade C.

To repeat: in 2014, as in other years, at least a quarter of a million 16-year olds finished 11 years of compulsory education unable answer all these questions.

Is this the best we can do? I hope not. Here’s some preliminary reflections and thoughts on this state of affairs.

Respect

‘Those who can, do. Those who can’t, teach.’

– George Bernard Shaw

‘Why on earth are you a teacher? I still don’t understand. You could’ve done so many things and you chose to become a teacher.’

– Multiple pupils

Respect in a profession is not the most important thing. Take rubbish collectors and lawyers, for example. Many jobs are not particularly respected – they may even be looked down upon – yet they nonetheless play an important part in society. They may even be relatively well compensated.

Nonetheless, respect is important. A respected profession is one which attracts high quality applicants. Given the teacher recruitment problems in the UK, it’s worth thinking about respect for the profession.

It’s also worth thinking about respect for the sake of well-being. Teachers are demotivated. While there are a huge variety of causes for this, a sense of general respect in teaching would undoubtedly help.

So, how respected are teachers?