The most useful hour I spent in my teacher training was at a talk on ‘Effective Explanations’ by Kris Boulton. The principle of minimizing cognitive load, which I learnt from him, has underpinned those lessons where my students end up telling me ‘this is actually really easy!’
However, for a while I’ve also been mulling on the research-backed principle of making tasks deliberately difficult to maximise learning. As Didau later writes, this principle seems to contradict the principle of minimizing cognitive load. How might we ‘square the circle’? It’s definitely worth reading the comment exchange between Kris and David here.
Here are some of my thoughts, developed as I’ve tried to work in both these principles into my teaching.
On my understanding, the idea behind minimizing cognitive load is this: we should focus all students’ working memory and effort upon the key thing that they fundamentally need to learn. Because working memory is limited, make sure that all cognitive load is directly related to the key learning objective. Reduce all noise and cognitive load that is irrelevant to the fact/process/concept in question.
So far so good. However – I believe some tasks can overly minimize cognitive load such that students aren’t thinking about/learning as much content as they need to. Here’s an example. Consider teaching the area of a triangle. I’ve chosen this topic as it’s a process that students regularly forget. So, what do students need to learn and remember? Something like: ‘When finding the area of a triangle, I need to identify a height perpendicular to a base, multiply them, then divide by two.’
My first port of call for quality questions is the MEP (which is usually excellent). There, I find questions like these:
Now, these questions apply minimal cognitive load: a student simply sees the measurements they need and can immediately apply the formula that they have learnt.
But here, in my thinking, is the problem. What does a student need to think in order to perform successfully at this worksheet? The most they need to think is simply this: ‘There are two numbers in the question. To get it right, I just have to multiply them and then divide that by two.’ If they can think and then perform this successfully, they should score 100%; they seem to be getting it. Now, as Willingham says, ‘memory is the residue of thought’. Therefore, from this task, the thought and memory formed might just be something as insubstantial as ‘find two numbers, multiply them and divide them by two’.
But that is nowhere near enough of what the student needs to remember. When we compare that thought to – ‘When finding the area of a triangle, I need to identify a height perpendicular to a base, multiply them, then divide by two‘ – two massive problems emerge.
- The task doesn’t force learners to engage with the fact that the formula only works with triangles. They see triangles; but the fact of the triangle is irrelevant to success in the task.
- The task doesn’t force learners to identify perpendicular heights and bases. They’re labelled; but their identification is irrelevant to success in the task.
So, a student might score 100% in this task yet completely fail to grasp some of the key aspects of finding the area of a triangle. Firstly, he may fail to link the process of ‘multiply together and divide it by two’ to triangles; therefore, the next time they see a triangle, that cue might not trigger the memory of this process. Secondly, when it comes to the following question, he might be completely stumped, since he has never had to identify the perpendicular height & base before.
So, in summary, the above task overly minimizes cognitive load such that the learning produced is insufficiently generalized, lacking in key content, and lacking a link to any cue.
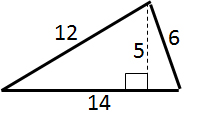
This is exactly where I think desirable difficulty comes in. In order for students to generalize sufficiently, produce the right memory hooks for the right cues, and substantiate concepts, extra difficulty and noise are necessary. They define the full extent and definition of the key thing students are meant to learn. Contrast the MEP task with Task 2:
Firstly, it is clear that this task brings a much higher cognitive load. There are twice the number of things to do – they’re asked to find perimeter as well as area; and there are twice as many numbers for students to deal with. But as I have just argued, this is exactly what is needed for students to form the thoughts and memories that they need to succeed: by asking for both area and perimeter, at every stage the task forces students to form a thought starting with ‘to find the area of a triangle I need to…’ – which creates the perfect hook for their memories that can then be activated when they encounter the cue ‘find the area of this triangle’. Secondly, the given slant heights force students to think ‘…I need to use the base and its perpendicular height‘, which is again exactly what they need to think and remember.
So in conclusion, despite the much higher cognitive load it brings, task 2 has desirable difficulties that bring sharp focus and clarity to the key thing that students need to learn. In my view, it is a much more effective task for learning the area of a triangle than the MEP task is.
A possible objection: what if task 2 simply imposes too high a cognitive load on certain groups of students, so they cannot engage? What if the price of the desirable difficulty is too high?
This may indeed be true. Yet it seems clear to me that the answer isn’t simply to go back to the first task. Instead, task 2 shows the sort of task that students ultimately must be able to succeed at, if we are to be confident that students have learnt what they need to learn. Furthermore, making such a ‘desirably difficult’ end-goal task then makes it clear what needs to be learnt beforehand. Students need to be confident in reciting / applying the formula, in how to find perimeters, and in identifying perpendicular heights & bases. For example, for a low-attaining class, doing the following task before task 2 would be a great idea:
Such a task would thus minimize the cognitive load of task 2 (especially if all the triangles were kept the same), and hopefully bring it within the reach of lower-attainers. Again it’s important to emphasise that this is a very different strategy to just giving the MEP task to those who struggle. In both cases, cognitive load is minimized. Yet one task minimizes cognitive load and leads to inadequate understandings and memories. The other minimizes cognitive load to focus on clearly defined essentials at each stage. (Bodil Isaksen writes excellently about that contrast here). Finally, even if students are sufficiently confident in finding perpendicular heights and perimeter, I think it’s also significant that Task 2 is still much more difficult than the MEP task; in this sense, these are real ‘desirable difficulties’ that increase cognitive load yet also increase learning.
In conclusion, to enable students to learn x, I believe we should include desirable difficulties in tasks to ensure that students are required to use everything they need to know about x in order to solve the task; students are thus forced to think about everything they’re meant to be think about to understand x correctly, and they thus embed those thoughts.
One final thought: from what I’ve heard and read about Shanghai pedagogy, they use desirable difficulties in instruction as well, for essentially the same reasons mentioned above – so that what students embed is the precise general concept that they need to learn.
As ever, would love to know how else this principle might be put into practise in other maths topics and more generally too. So far, my main general idea is that wherever possible, introduce unnecessary/distracting information into questions. Let me know your thoughts and reflections.



I’m not a teacher. I think I follow what you mean. I remember that the area of a triangle is 1/2 x base x height. This is easy to remember, but to actual solve calculations I then need to apply these terms appropriately. I wonder if this (though quite subtle) difference to the area of a triangle formulation you give above, would serve the purpose of focussing the students on everything they needed to consider in the task to get the maximum benefit from it?
LikeLike
Hi chemistrypoet, thanks for your comment.
Indeed, remembering a formula and using it correctly in all applicable situations are very different things.
However, I don’t think it’s enough just to learn the formula in terms of perpendicular height. I believe that tasks and questions must then force students to identify and use the idea of ‘perpendicular height’, so that this concept is thought about and then embedded in memory. This is where the desirable difficulty comes in useful.
LikeLike
To be honest, I’d give both tasks. Or rather, the resource I use looks like a mix of the two. I think the way we square the circle of low cognitive load (which is about grasping the idea in the first place) and desirable difficulty (which is about recalling it afterwards), is to use tasks that start easy and get harder.
LikeLike
Of course that would work well too. One interesting thing is that the MEP task, and many like it, don’t really get any harder for triangles per se. It goes straight onto compound shapes, which is more difficult, but not in a way that tests out one’s knowledge of triangles. The way it gets difficult matters a lot.
LikeLike
Pingback: Mathagogy: how to introduce the balance method for solving equations | mathagogy
Pingback: Mathagogy: how to introduce the balance method for solving equations | mathagogy
Pingback: Mathagogy: adding and subtracting negative numbers | mathagogy
Squaring is not necessary.
Cognitive Load Theory does not state that less load=best. Both germane load as existing research on schema building indicate that it should be about successful integration into schemas.
This fits in with all kinds of worthwhile processes Didau set out in his blog and fading, scaffolding etc. One mechanism can also be ‘desirable difficulties’ or intentional crises (perturbations, cognitive conflicts, productive failure). Yes they might (intentionally) spark load but they are conducive to schema building.
This should not be a random difficulty but a carefully designed one, a bit like Variation Theory in Asian countries (and work with example by Mason and Watson in UK) does.
Just some thoughts.
LikeLiked by 1 person
Thanks for the thoughtful comment. I’m not at all an expert in the academic literature, so I appreciate your insights. I will definitely have a look at schema building – any recommendations for things to read?
LikeLike
The original germane load in CLT, rumour has it though that Sweller has denounced it, has entries into schemas (Pass, Merrienboer). Dare I say it, Wikipedia page schemas is decent. But best book, although not sure any more if uses exact same word but idea same, Ohlsson on Deep Learning is relevant cognitive psychology. Keep up the nice blogs!
LikeLike
Pingback: Efficacy, efficiency, and mastery | mathagogy
Pingback: Germane load: linking processes with their names | mathagogy
Pingback: The descriptive principle that learners minimize their cognitive load | mathagogy
Pingback: Is this the best we can do? Part 4: better pedagogy through better textbooks | mathagogy
Pingback: Teaching mathematical grammar | mathagogy