In 2014, 62.4% of teenagers sitting GCSE maths achieved at least a grade C – the ‘gold standard’ grade needed to progress onto a wide range of further study and employment. For the last 5 years, the pass rate has hovered around 60%.
The flipside of this statistic: every year, at least 40% – that’s a quarter of a million 16-year olds – complete their secondary education without having attained a C in GCSE maths.
Is this the best we can do?
I looked at the 2014 GCSE Higher maths papers. To have gotten a grade C in it, you needed 57 marks out of 200 (a statistic that shocked me when I first discovered it, and continues to shock). Below are 63 marks’ worth of questions from 2014’s two papers (click to enlarge) – if you got all of these questions right, give or take 2-3 of them, you would’ve done enough to get that coveted grade C.
To repeat: in 2014, as in other years, at least a quarter of a million 16-year olds finished 11 years of compulsory education unable answer all these questions.
Is this the best we can do? I hope not. Here’s some preliminary reflections and thoughts on this state of affairs.
Firstly, it is true that the A*-C pass rates have been steadily increasing. 10+ years ago, the average was closer to 55%; 15+ years ago, it was around 50%; 20+ years ago, it was around 45%.
But several things outweigh any premature optimism. There’s a widespread view, even(/especially?) among teachers, that exams have gotten substantially easier in this time frame. For example, “Hannah’s sweets”, the infamous ‘impossible’ question in last year’s paper, was perceived as unreasonably difficult for GCSE maths. Students across the country were furious. Yet as others have pointed out, an essentially identical question came up in 2002, to zero fanfare across the country. Of course, as the link points out, that may be due to our social media age where teenagers have more of a public voice than ever before.
So let’s look at some cold hard data: this graph (found here) always makes me think long and hard:
In short: while GCSE test performance has shot up (the thick mauve line), other internationally-used measures of maths performance have shown practically zero improvement in English students’ mathematics skills over the past 15 to 20 years.
To be fair to schools, I don’t think the increase in performance is solely due to easier exams. I looked at GCSE maths papers from 2006, and didn’t notice any substantial differences in difficulty to maths papers written according to our modern specification – yet the A*-C pass rate in that year was 54.3%. What’s happened in maths education in the past 10 years to create that 10% pass rate increase? And why hasn’t that translated into improved maths performance in international measures?
Alongside an easier, more accessible curriculum, there’s been a massive improvement in technology and ability to access and compare past papers (compared to the rows of filing cabinets we used to use to store past exam materials). Across education technology’s influence has also been since in the rise of data and data-driven accountability. These two trends are relevant as they have given rise to a much more detailed understanding of examinations and examination trends. The PiXL Club, founded around 2010, is the culmination of these trends: a group that regularly receives accusations of ‘gaming’ the examination system to improve school outcomes.
At individual school level, the picture looks similar. The last decade or two has seen the rise of exam-centred intensive intervention as the norm for any ambitious school. At any school attaining above average GCSE maths pass rates, each year you’ll see a massive resource focus on y11: the Christmas mock, where borderline students are identified; Spring term & Easter holiday intervention sessions; after school maths clubs; the same 30 topics recycled again and again; the same folders of past paper topic sheets printed out. As for years 7-10, it doesn’t seem that important: as long as they receive okay teaching and cover most of the curriculum, they will have done enough to make the grade in year 11.
That, as far as I can see, is the strategy of the past 10 years: an increased familiarity with exams and how to position students to tackle them best. Many schools have significantly exceeded the 60% national pass rate, and this approach seems to be the core of their strategy.
Why does it work so well? Well, consider those 57 marks needed for a GCSE grade C. None of those questions require any serious thinking – they are all straightforward questions that rely heavily on the memory of seeing and answering similar questions in exam practise. Since they are not difficult, they are the sort of thing that 90+% of people could get to grips with in a year’s intense study. And so, intense intervention is the way forward.
This is all intended as factual – I don’t mean to be critical. The increase to a 60% pass rate has resulted in hundreds of thousands of people facing life with one less barrier in their way. That is an indisputably good result.
But then I look again at the graph, showing our country’s maths performance outside of the GCSE; and again I wonder: is this the best we can do? When English students take the international comparison assessments, they are faced with questions that require serious thinking – the sort of careful, logical thinking that actually tests their thinking skills (compare to some of the C-grade questions above) – and the data clearly shows that we haven’t gotten any better in teaching them how to think mathematically.
That’s despite my sense that we’ve exploited most of the possible gains in the maths-intervention-exam-preparation technique. Of course, other schools (for example those with severe shortage of maths teachers) could have still benefited from it – but by and large, successful schools know what to do each year to get them those 70%-80%+ pass rates. There isn’t much room for further innovation there: it’s mainly a case of rolling out its implementation.
More worryingly, our mediocrity in international assessments might soon become seen in national assessments too. From the looks of the new, more difficult curriculum, it seems clear to me that maths-intervention-exam-prep will soon lose most of its power. The increased focus on non-routine problem solving doesn’t seem to be something that can easily be taught and then drummed over 9 months of year 11.In other words, the benefits from y11 intervention techniques, perfected in the past 10-20 years, aren’t well suited to the new GCSE. We’re going to have to try something else – something radically different. Do any schools feel truly prepared?
To bring things back around full circle, my first prompting thought for this post was this: how could any (let alone a quarter of a million) 16-year olds fail to get those 60 marks? I then digressed into the methods used for a national improvement in the pass rate… but that first question still stands. What about those students from the past 15 years who, despite an intense 9 months of year 11 intervention, still failed to get those 60 marks? Why couldn’t they get quite over the line?
My final reflection: this problem could stem from the same intense-intervention focus that has led to such success. Why? The GCSE is meant to be the summation of 11 years of compulsory mathematics education. Yet the vast majority of attention and effort nationally is focused on two years: year 6, and year 11. The relative ease of getting a GCSE C-grade meant that many students were actually fine to achieve this with 9 months’ intense focused study; but understandably, many students might not be able to achieve this in such a short space of time. In short, fitting in 11 years of maths curriculum all into one high-stakes year might be asking too much for those students who fail. The intense intervention approach might just be totally ill suited for many students. Indeed, to view the problem from another angle, a better question to ask ourselves (instead of looking at GCSE pass rates) might be: how do so many hundreds of thousands 15-year olds enter year 11, after 10 years of compulsory maths, at a grade E (or worse) level of maths? Is this the best we can do?
In my next posts I’ll think a bit more about possible roots of this problem, some solutions that are commonly offered, and some strategies which strike me as promising ways forward. Any of your own diagnoses and suggestions would be most welcome – do leave a comment below.
UPDATE: On Twitter many people have commented on the way GCSE pass rates are norm-referenced, as opposed to criterion referenced. Several have mentioned the argument that even if 16 year olds’ mathematics performance in the UK suddenly improved one year, Ofqual/exam bodies/the government would ultimately decide to keep the pass rate roughly level according to their own judgments. So, my argument doesn’t work: the question of improving the UK maths education system is, apparently, not particularly linked to the separate question of how many students receive C-grade passes in any given year.
For brevity’s sake, my responses will grant this argument: it nonetheless remains true that ~40% of students, each year, fail to accumulate the marks from questions like those I posted above. That continues to stagger me. Is this outcome (regardless of grading) the best that 11 years of maths education can do for 40% of the country’s young people?
Secondly, we could recast my argument in terms of the PISA/TIMMS performance measures, which (as far as I know) are criteria-referenced and much easier to form a judgment from. As one of the most highly educated, developed, prosperous countries in the world, is our PISA ranking the best we can do? That question still remains, regardless of how GCSE pass rates are determined.
- Click here for Part 2: Diagnosis
- Click here for Part 3: Success stories
- Click here for Part 4: Better pedagogy through better textbooks
- Click here for Part 5: Hard work and homework



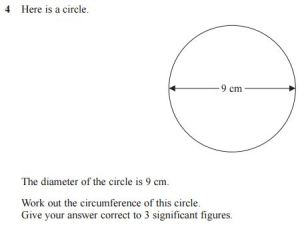


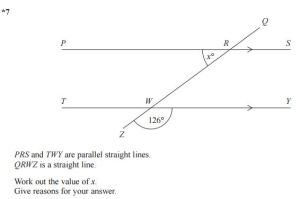














I don’t think the GSCEs have been norm-referenced since 2008. They will be from 2017 however. That argument is easy to refute though, in that in a norm-referenced system we would see grade boundaries increase if average performance were to increase, so we could still observe an improvement in raw attainment.
LikeLike
Thanks. I’m not familiar with the details of GCSE marking myself, hence my own reply that even if it is true, the underlying problems are still there. I like your response too.
LikeLike
Pingback: Is this the best we can do? Part 2: Diagnosis | mathagogy
If norm referencing was abandoned in 2008, and alongside that primary maths teaching improved – as the results for timms 10 yr olds seems to indicate, then wouldn’t a massive surge in GCSE results be expected and be legitimate once the norm reference ‘cap’ on percentages achieving each grade was lifted?
LikeLike
Pingback: Is this the best we can do? Part 3: success stories | mathagogy
Pingback: Is this the best we can do? Part 4: better pedagogy through better textbooks | mathagogy
Reblogged this on The Echo Chamber.
LikeLike
Pingback: Is this the best we can do? Part 5: hard work & homework | mathagogy
Pingback: Repeat After ‘E’: the treadmill of post-16 GCSE maths and English retakes – Education Datalab
Pingback: Is this the best we can do? Part 6: the problem of forgetting | mathagogy
Pingback: Is this the best we can do? Part 7: the spacing effect | mathagogy